Support Vector Regression

Support Vector Machine(이하 SVM)이 margin을 최대화 함으로써 Classification을 잘 하게 하는 알고리즘이라면 Support Vector Regression(이하 SVR)은 같은 원리로 Regression을 잘 하게 한다.

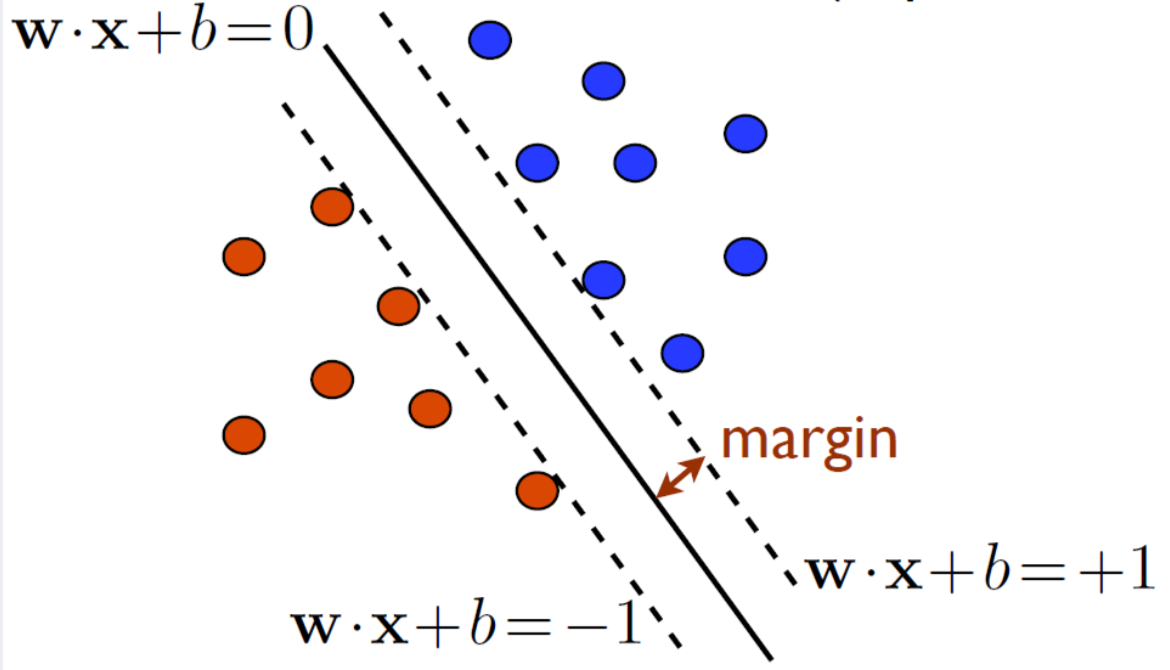
위의 figure1에 따르면 SVM의 경우 hyperplane은 각 점(분류하고자 하는 data point들)을 두 class로 나누어준다. 반면 SVR의 경우 hyperplane은 data를 가장 잘 표현해주는 line이다.

Linear Regression

Linear Regression이란 data를 기반으로 X와 Y의 관계를 가장 잘 표현하는 linear function을 찾는 것이다. 즉, $y = \mathbf{w}\cdot\mathbf{x}+b$ 에서 loss를 최소화하는 $\mathbf{w}, b$ 를 찾아야한다. 이 때의 loss function은 주로 sum of squared error이다. 주어진 모든 data { $\mathbf{x}_{i},{y}_{i}$ } 에 대해 우리가 function으로 예측한 $\hat{y}$ 와 실제 $y$ 간의 차이를 최소화 하는 것이다.

$min \sum _{i=1}^{m}({y}_{i}-\hat{y}_{i})^{2} = \sum _{i=1}^{m}({y}_{i} - (\mathbf{w}\cdot\mathbf{x}_{i}+b))^{2}$

이제 이러한 Regression Problem을 SVM의 방식을 차용해 풀어내는 SVR에 대해 본격적으로 알아보자.

$\epsilon$ -SVR

Regression의 loss function을 어떻게 정의하느냐에 따라 SVR의 모델도 다양하게 정의될 수 있지만, 이 포스트에서는 가장 대표적인 $\epsilon$ -insensitive loss function을 사용한 $\epsilon$ -SVR에 대해 살펴보겠다.

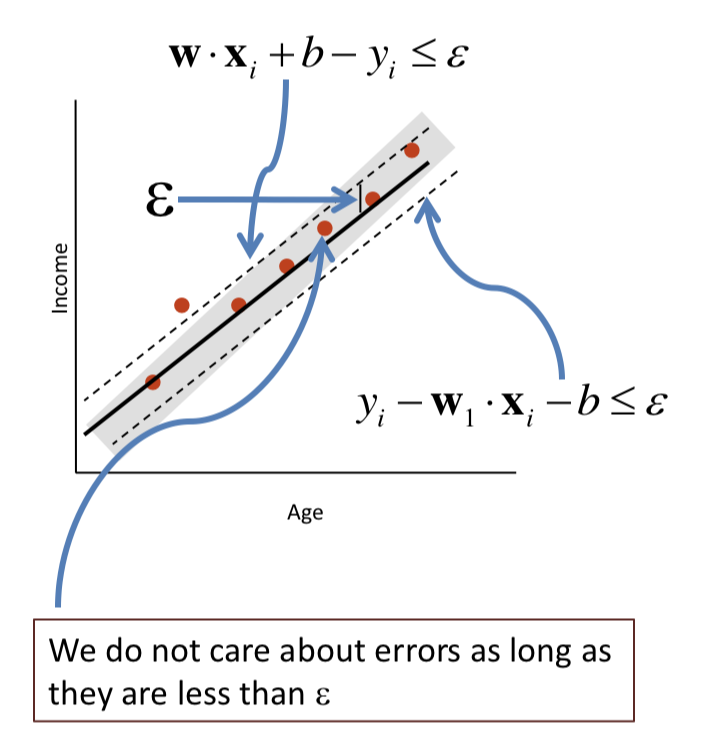
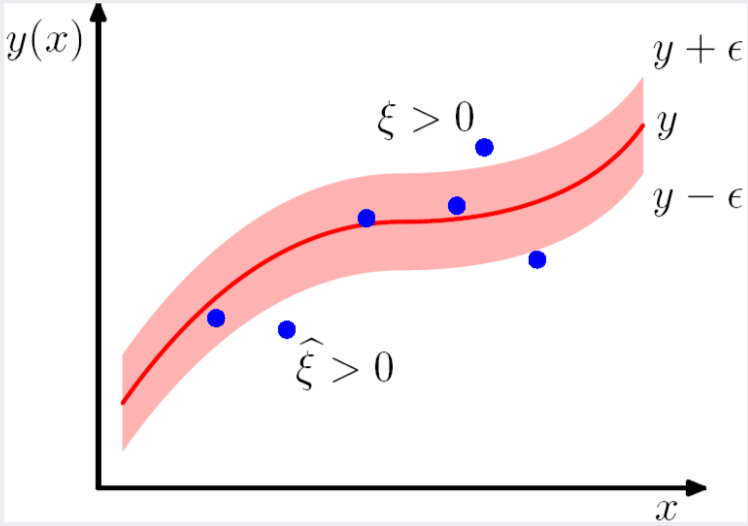
첫 번째 그림의 예시는 나이와 월급의 관계를 설명하는 최적의 line을 찾는 예시이다. 실제 data Y와 line의 예측값 간의 차이를 loss function으로 삼아 최소화 하는데, 이 때 $\epsilon$ -insensitive 의 의미는 그 차이가 $\epsilon$ 이하 일 때는 loss를 0으로 취급한다는 것이다.

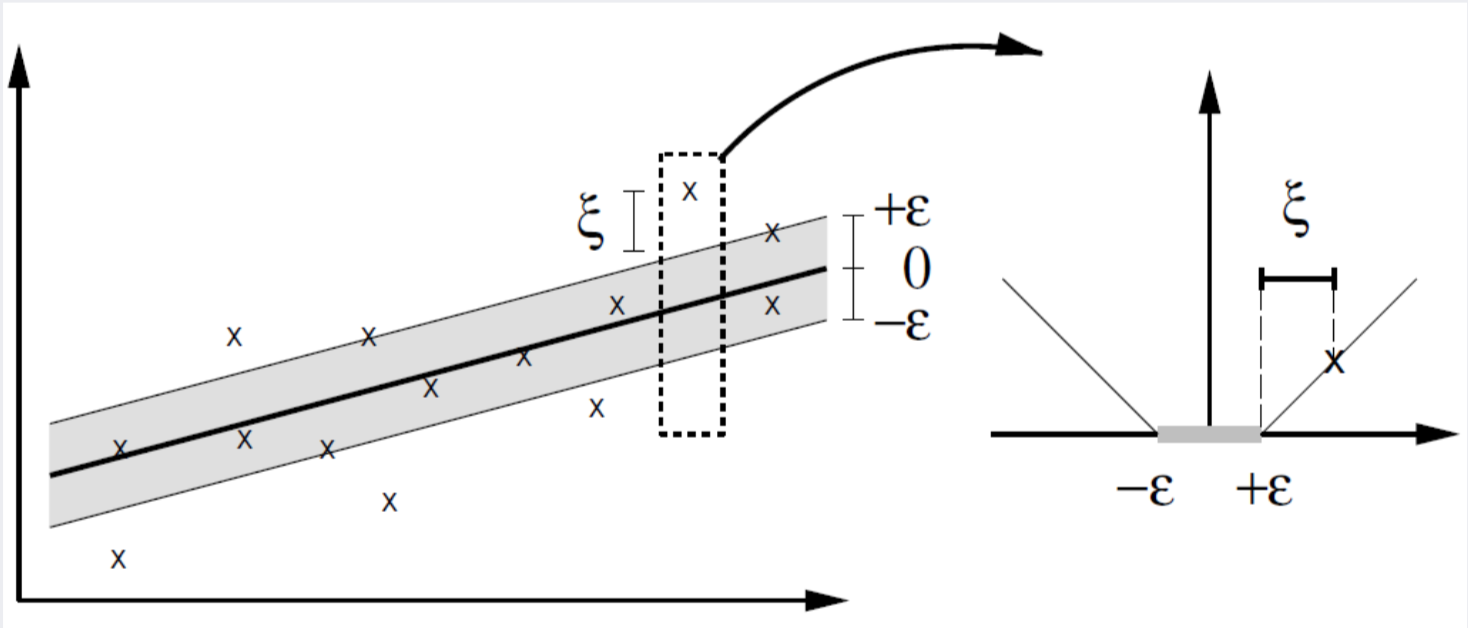
두 번째 그림에서 보듯이 모델의 예측값 $\hat{y}$ 과 타겟값 ${y}$ 의 차이가 $\epsilon$ 이상일 때만 loss에 반영이 된다. $\epsilon$ 을 넘어서는 차이를 $\xi_{i}$ 로 표현한다.

우선 우리가 가진 data를 가장 잘 표현하는 hyperplane $f(x)$ 를 정의해 보았다. 단순한 일차식이지만 추후 kernel trick의 적용을 통해 non-linear한 hyperplane을 만들 수 있다.

$f(\mathbf{x}) = {\mathbf{w}^{T}\mathbf{x}} + {b}$

최적의 $f(x)$ 를 찾기 위해 우리는 다음과 같은 목적 함수를 풀어야한다.

$min \frac {1} {2} \lVert \mathbf{w} \rVert^{2} + {C}\sum _{i=1}^{n}(\xi_{i} + \xi_{i}^{*})$ ${s.t.} ( \mathbf{w}^{T}\mathbf{x}_{i} + {b} ) - {y}_{i} \le \epsilon + \xi_{i}$ $\quad {y}_{i} - ( \mathbf{w}^{T}\mathbf{x}_{i} + {b} ) \ge \epsilon + \xi_{i}^{*}$ $\quad \xi_{i}, \xi_{i}^{*} \ge 0$

식의 첫 번째 부분은 SVM에서와 같이 margin을 극대화하여 모델의 일반화를 가능하게 해주는 부분이다.
두 번째 부분은 $f(x)$ 의 위 아래로 margin만큼의 간격을 갖는 decision boundary 밖에 일부 data가 있더라도 그 $f(x)$ 가 가장 margin을 최대화한다면 그 solution을 취하려는 soft margin을 도입하면서 생겨난 부분이다. 이 때, $\xi_{i}$ 는 fitting line에서 떨어진 정도를 나타내며 이를 최소화한다는 것은 오류를 최소화한다는 말이다.

열거된 세 개의 조건문을 살펴보면 어떻게 SVM을 활용한 regression 모델의 loss function이 어떻게 작동하는지 자세히 알 수 있다. $\xi_{i}$ 와 $\xi_{i}^{*}$ 은 모델 $f(x)$ 과 실제 data의 차이가 $\epsilon$ 이상인 data point에 한해 정의된다. $\xi_{i}$ 와 $\xi_{i}^{*}$ 는 각각 모델 $f(x)$ 의 위와 아래에 위치할 경우를 나누어 놓은 것이다.

목적함수를 Primal Lagrangian 으로 변환하면 다음과 같다.

${L}_{P} = \frac {1} {2} \lVert \mathbf{w} \rVert^{2} + {C}\sum _{i=1}^{n}(\xi_{i} + \xi_{i}^{*}) - \sum _{i=1}^{n}( \eta_{i}\xi_{i} + \eta_{i}^{*}\xi_{i}^{*})$ $- \sum _{i=1}^{n} \alpha_{i}(\epsilon + \xi_{i} + y_{i} - \mathbf{w}^{T}\mathbf{x}_{i} - b) - \sum _{i=1}^{n} \alpha_{i}^{*}(\epsilon + \xi_{i}^{*} + y_{i} - \mathbf{w}^{T}\mathbf{x}_{i} - b)$ $\alpha_{i}^{(*)},\eta_{i}^{(*)} \ge 0$

Non-linear SVR

x를 고차원 공간으로 mapping 시켜주는 kernel trick을 적용하여 고차원 상에서 non-linear한 hyperplane을 가능하게하는 Non-linear SVR로 넘어가자. kernel trick을 적용한 Dual Lagrangian 목적식은 다음과 같다.

${L}_{D} = - \frac {1} {2} \sum _{i,j=1}^{n} (\alpha_{i}^{*}-\alpha_{i})(\alpha_{j}^{*}-\alpha_{j})K(\mathbf{x}_{i},\mathbf{x}_{j}) - \epsilon \sum _{i,j=1}^{n} (\alpha_{i}+\alpha_{i}^{*}) + \sum _{i,j=1}^{n} y_{i}(\alpha_{i}^{*}-\alpha_{i})$
$\quad {s.t.} \sum _{i=1}^{n}(\alpha_{i}-\alpha_{i}^{*}) = 0, \quad 0 \le \alpha_{i},\alpha_{i}^{*} \le C$

Code Implementation

이제 python으로 작성된 코드와 함께 어떻게 non-linear SVR 문제를 해결하고 새로운 data에 대해 regression 예측을 할 수 있는지 살펴보자. data는 sine function에 약간의 noise를 추가하여 생성하였고 x축이 time, y축이 weight이라고 가정했다. 시간이 흐름에 따라 몸무게가 어떻게 변화하는지를 예측하는 regression 모델을 만들어보자.

# Generate sample data
X = np.sort(10*np.random.rand(100,1),axis=0)
y = np.sin(X).ravel()
print(y.shape)
y[::5] += 5*(0.5-np.random.rand(20))
y[::3] += 2*(0.5-np.random.rand(34))

plt.scatter(X, y, color='red', label='data')
plt.xlabel('time') 
plt.ylabel('weight')
plt.title('data')
plt.show()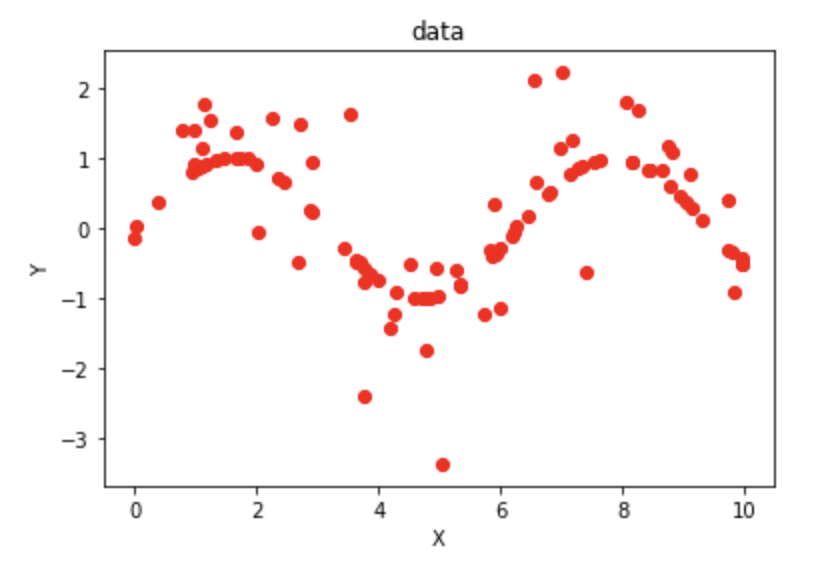

SVR에서 중요하게 생각되는 파라미터는 크게 C, $\epsilon$ , kernel 함수가 있다. 각 파라미터의 영향에 대해서는 이후의 결과부분에서 보다 자세히 설명할 것이다.

이 코드에서는 cvxpy라는 모듈을 사용하여 lagrangian problem을 풀고 있다. 먼저 위의 Non-linear SVR 파트에서 소개된 svr의 objective function을 코드로 작성하고 Dual Lagrangian problem이기 때문에 이를 maximize하도록 목적함수를 지정해준다. 이와 함께 constraint들을 코드로 만들어준다. 그리고 정의된 Problem을 solve function을 통해 풀 수 있다. 이 때 kernel 함수는 rbf를 이용했다.

# hyperparameter settings
C = 1
epsilon = 1.0

#variable for dual optimization problem
n = X.shape[0]
alpha = cvx.Variable(n)
alpha_ = cvx.Variable(n)
one_vec = np.ones(n)

# model objective
obj = -.5*cvx.quad_form(alpha-alpha_,kernel_mat(X,kernel='rbf',gamma=0.1))\\
	  - epsilon*one_vec*(alpha+alpha_) + y*(alpha-alpha_)
svr_obj= cvx.Maximize(cvx.sum(obj))

# model constraints 
constraints = []
constraints += [cvx.sum(one_vec*alpha - one_vec*alpha_)==0]
for i in range(n): 
    constraints += [alpha[i]>=0, alpha_[i]>=0, alpha[i] <= C, alpha_[i] <=C]
    
    
svr = cvx.Problem(svr_obj, constraints)
svr.solve()

# kernel function : rbf kernel
def rbf_kernel(x1,x2, gamma=0.1): 
    return np.exp(-gamma* abs(x1-x2)**2)

# gram matrix 
def kernel_mat(X,coef0=0.0,degree=3,gamma=0.1):
    X = np.array(X,dtype=np.float64)
    mat = []
    for i in X:
        row = []
        for j in X:
            row.append(rbf_kernel(i,j,gamma)[0])
        mat.append(row)
    return np.array(mat)

Result

SVR이 예측한 regression 모델은 아래 그림과 같다. 빨간 점은 data이며 검은 선이 regression line, 두 회색 선은 epsilon-insensitive 영역을 표현한다.

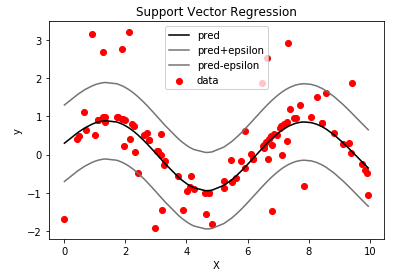
앞서 언급했듯이 SVR에서는 C, $\epsilon$ , kernel 함수 등 hyperparameter 설정에 따라 모델의 일반화 성능이 크게 달라진다. 적절한 hyperparameter 설정이 중요한 이유는 모델의 복잡도와 모델의 일반화 능력 사이의 절충을 해야하기 때문이다.

parameter C 는 $\epsilon$ 보다 큰 오차를 얼마나 수용할지를 정한다. 즉, C가 큰 경우 오차에 큰 가중치가 붙기 때문에 모델은 최대한 data에 맞추어 outlier일지라도 수용할 수 있도록 모델의 complexity를 높일 것이다. 이는 SVM의 강점인 모델의 일반화 성능을 감소시킬수 있다.

parameter $\epsilon$ 은 $\epsilon$ -insensitive 영역의 넓이를 결정한다. $\epsilon$ 이 클수록 많은 데이터가 epsilon-insensitive 영역에 놓이며 loss function에 관여하는 support vector의 수가 적어진다. 아래의 figure5에서 확인할 수 있듯이 $\epsilon$ 가 클수록 모델 복잡도는 낮아지며 좀 더 flat한 모델을 얻을 수 있다.

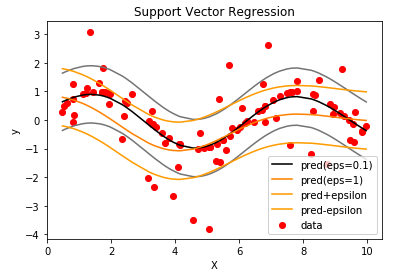
Reference